DontPayFull.com

Prin labiriturile matematicii

Cum a inceput sa ma intereseze sa numar labirituri?

O serie de evenimente fericite

1982

Prima mea intâlnire cu aceste labirinturi a fost in jurul anului 1982, cand labirintologul Jean-Louis Bourgeois mi-a aratat jocul cu labirinturi. Mi-a spus ca acest joc este raspandit in culturile populare din Asia; Este extrem de veche, deoarece acest design se intampla si pe monedele cretan din secolul IV-V I.H., unde simbolizeaza labirintul in care a fost pastrat Minotaurul. (De fapt, exista exemple mult mai vechi) Legenda spune că Tezu a iesit din labirint urmand un fir pe care l-a desfasurat dintr-o bobina data de iubita lui Ariadne si astfel a trasat o linie sa traseze calea printr-un labirint ca acesta, este deseori numit "firul lui Ariadne.''

In scurt timp, am vizitat casa lui David Gay, un matematician de la Universitatea din Arizona din Tucson. Atarnand de perete, era un cos plat, de circa 18 cm in diametru, tesut cu un design care sa dovedit a fi identic din punct de vedere topologic cu labirintul cretan. David mi-a spus ca acest design de cos este traditional cu To'ono-Otum (initial Papago) indieni, un trib care traieste acum in Arizona de Nord si ca intorsaturile si rasucirile traseului prin labirint reprezinta evenimente si incercări in viata eroului Iitoi prezentat la intrare.

1983

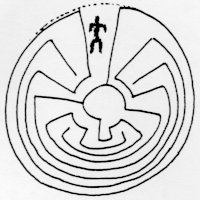
In cele din urma, cateva luni mai tarziu, vizitand parintii mei in Florida si framantand prin catalogul lui Sotheby, am fost lovita de fotografia unei pagini dintr-un manuscris medieval evreiesc (Sefer Haftorot), care urma sa fie vandut pe 23 iunie 1983. Fotografia a aratat acest design:

Labirint de la un medieval Sefer Haftorot.
 

Cei sapte pereti concentrici simbolizeaza cele sapte ziduri ale Ierihonului. Cuvintele din Psalmul 104, vv. 1-18, 20, 21 vant de-a lungul caii. In centru este scris "Jericho" si "Imaginea zidului Ierihonului. Cititorul este ca si cum ar fi mersul pe jos. "(Multumită Prof. Robert Goldberger pentru traducere.) Fotografie obtinuta prin amabilitatea lui Sotheby's Inc., New York.

Desi acest labirint are o asemanare superficiala cu labirintul cretan, o comparatie apropiata arata ca acestea sunt destul de diferite. Labirintul Jericho are 7 nivele, in timp ce labirintul cretan are 8, iar secventa in care sunt atinse nivelurile este destul de diferita de la un labirint la altul. In ambele labirinturi, calea merge direct la nivelul 3 (numarati exteriorul ca 0), dar in labirintul cretan se dublează apoi prin nivelele 2 si 1, in timp ce in labirintul din Jericho continua prin nivelurile 4 si 5 înainte de a reveni la 2 si 1. Secventele de nivel complet sunt

Cretan  0 3 2 1 4 7 6 5 8

            Jericho  0 3 4 5 2 1 6 7.

Acestea pot fi interpretate ca fraze muzicale, permitand 0 = C, 1 = D etc. Urechea detecteaza imediat ca, in tonul cretan, fraza initiala se repeta intr-un pas mai inalt; Dupa cum am inteles mai tarziu, acest labirint poate fi descompus in produs sau stivuirea a doua copii ale labirintului de patru niveluri 03214.

Dupa ce am vazut doua exemple similare, dar distincte, am inceput sa ma intreb cat mai multe ar putea exista. Primul lucru era să intelegi exact ce au avut in comun. Se pare ca exista trei caracteristici pe care le impartasesc si care definesc o clasă de labirinturi care pot fi investigate matematic: acestea sunt labirintele simple, alternante, de tranzit. Am devenit interesat de problema determinarii lui M (n), numarul de s.a.t. Labirinturi cu nivel n.

1985-86

Pana atunci, petreceam un sabat in Italia, unde Michele Emmer, profesor la Universitatea din Roma, se intâmpla sa faca una dintre filmele sale de matematica / arta, cu privire la labirinturi. Ma invitat sa apar in film si sa vorbesc despre s.a.t. Labirinturi, asa ca am scris un scenariu pentru mine, care este baza acestui text. In scenariu am explicat cum puteti afla care permutari ale numerelor intregi pot fi secvente de nivel ale s.a.t. labirinturi. (Acest lucru a fost lasat in afara filmului.)

1986

In decembrie 1986, am fost la Paul Erdös la o petrecere si i-am spus despre interesul meu fata de acest fenomen combinatoric. El ma intrebat daca numarul M (n) pare sa fie in crestere exponentiala sau chiar factoriala cu n. Aceasta conversatie scurta ma facut sa ma gandesc la comportamentul functiei M (n). Am reusit sa-i scriu o saptamana mai tarziu ca numarul I (n) de labirinte interesante creste cel putin exponențial cu n. Dovada a aratat prin constructie ca I (n + 4)> = 6I (n); 6 poate fi imbunatatit la 8 dupa cum urmeaza: pentru fiecare labirint interesant de adancime n, cele 8 labirinturi de nivel (n + 4) aratate aici

Fiecare labirint n-nivel interesant da nastere la 8 labirinte interesante diferite de adancime n + 4; In b, g, h calea trece prin labirint n-nivel inapoi.

sunt toate interesante, iar aceste noi labirinturi sunt toate distincte. In aceasta figura, labirinturile sunt reprezentate de caile lor de labirint in forma dreptunghiulara. Retineti ca labirintul initial n-nivel are loc atat cu intrarea in dreapta, cat si pe partea stanga. Dovada ca aceste labirinturi distincte necesita o ipoteza "interesanta".''

Apoi am inceput sa caut un mod de calcul M (n). Metoda pe care am folosit-o nu era practica pentru valori mai mari de n, deoarece implica cautarea unui numar de perechi de permutari care au crescut, aproximativ, ca ((n / 2)!) ^ 2. Pentru a calcula M (20), de exemplu, ar fi nevoie de examinarea a aproximativ 10 perechi (13), ceea ce ar dura mult timp chiar si pe un calculator foarte rapid. Ajutorul a sosit dintr-o sursa neasteptata.

1987

In sectiunea Stiinte New York Times pentru marti, 27 ianuarie 1987 a fost un articol al lui James Gleick despre matematicianul Neil JA Sloane, care a inceput: "Fara inteles, Neil JA Sloane a devenit casa de compensare a lumii pentru secvente de numere . El tine evidenta celor usoare, cum ar fi 1, 2, 4, 8, 16, 32 ... puterile a doua. El tine evidenta celor grele, cum ar fi 1, 1, 2, 5, 14, 38, 120, 353 ... numarul de moduri diferite de pliere a unor benzi de timbre postale. ...''

Acesta a fost primul care am auzit vreodata de problema de pliere a stampilei, dar este in mod clar legata de problema de a numara labirinturi. De fapt, fiecare labirint de adancime n da o modalitate de pliere a unei benzi de stampile n + 1: pune labirintul in forma dreptunghiulara si pune timbrele de-a lungul labirintului, cate unul pe fiecare nivel (inclusiv 0 si n), ignorand verticala segmente. Dar exista o diferenta: prima si ultima stampila a unei benzi pliate poate avea marginile libere inglobate in interiorul pachetului, in timp ce primul nivel (după 0) si ultimul nivel (inainte de n) al unui labirint trebuie sa fie. Au capetele libere pe exterior. Deci, daca F (n) este numarul de cai de pliere a unei benzi de stampile n, putem

concluziona numai ca M (n)

Calculul lui F (n) a fost facut de catre John E. Koehler, SJ pentru n <= 16 intr-un articol publicat în 1968. Numerele incep de la F (16) = 4215768. Dar cel mai util a fost Ca Koehler a descris o modalitate de a numara plierea unei benzi de stampile n (n chiar) prin cautarea perechilor de "n-modele"; iar numarul de n-modele distincte a fost disponibil in forma inchisa, pentru n chiar: A fost numarul (n / 2) catalan Cat (n / 2). S.a.t. Mazes cu n nivele admit o enumerare similara; In acest caz cele doua n-sabloane trebuie sa satisfaca conditia suplimentara care garanteaza o singura cale de filetare a intregului labirint. Acum numerele catalane, chiar daca ele sunt definite cu factoriali, cresc doar exponential; de fapt

k  -3/2   -1/2
        Cat(k) ~  4  k     pi
	

Pentru k mare, o consecinta usoara a formulei lui Stirling. Rezulta ca, deoarece fiecare labirint n-nivel corespunde unei perechi de n-sabloane, numarul M (n) al labirinilor n-nivel (n egal) este <= Cat (n / 2) ^ 2 exponential.

Mai practic, exista mai multe perechi de n-modele mai putine decat perechile de permutari ale elementelor n / 2, iar identificarea lui Koehler mi-a permis sa calculez M (n) prin n = 22 pentru n chiar prin verificarea tuturor perechilor n- Proprietatea cu un singur ciclu. Desigur, timpul de calcul continua sa creasca exponential cu n. Pentru n = 22 numarul de perechi de n-modele de examinat a fost Cat (11) ^ 2 = 3455793796. Aceasta a durat aproximativ 73 de ore pe un calculator Sun-3. Calculul n = 24 ar dura aproximativ 16 ori

mai mult, etc.

Jim Reeds of Bell Labs a gasit o metoda mai buna si a reusit sa extinda calculul la n = 28.

Un produs secundar al studierii mele asupra acestor modele de labirint a fost realizarea faptului ca producatorii de labirint din vremurile antice au lucrat prin combinarea unui numar limitat de forme fundamentale. Acest lucru mi-a permis sa sugerez cum ar trebui restaurate partial distruse labirinturi romane de mozaic si sa se detecteze cateva exemple de restaurare defectuoasa a celor deja reparate. Vezi topologia labirinturilor romane de mozaic.