Fizica de baza a canotajului

Modificari recente

(Parte din Fizica Canotajului)

• 13DEC07 Proiectat si proiectat actualizat.

1. Propulsie

O barca accelereaza prin principiul actiunii / reactiunii (Legea a treia a lui Newton). Daca trageti apa intr-o directie cu vasla, barca se misca invers. Momentul (= masa x viteza) pe care il introduceti in apa va fi egal si opus momentului dobandit de barca.

Luati in considerare o barca inainte si dupa o vaslire.

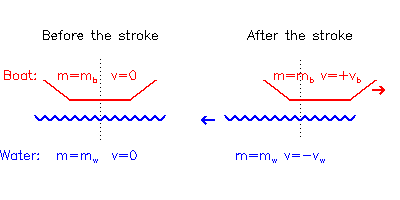Figura (1.1)

Inainte de cursa, impulsul total p = 0, deoarece totul este in repaus.
Dupa vaslire, impulsul total: p = mbvb - mwvw = 0 deoarece impulsul total nu se poate schimba (Legea a2a lui Newton ).

De exemplu. Pentru o barca + masa echipajului mb = 100 kg (adica un singur sculler) pentru a accelera de la repaus la vb = 1 m / s, necesita fie mw = 10 kg apa care urmeaza sa fie accelerata la vw = 10 m / s, sau mw = Kg apa pana la vw = 5 m / s sau orice alta combinatie de mw si vw care da produsul mwvw = mbvb = 100 kg m / s.

In timpul cursei normale (adica cu barca deja in miscare) este mai putin evident ca apa este mutata inapoi pentru a mentine barca in miscare inainte, deoarece lamele par sa "se blocheze" in locul in care sunt plasate, dar daca va uitati la balti cand se extrag lamele, este clar ca apa este miscata. Trebuie sa existe o alunecare pentru a accelera barca, desi, din considerente energetice (sectiunea 3), aceasta ar trebui sa fie cat mai mica posibil.

Deci, daca impingi fundul raului sau  o serie de stalpi plantati de-a lungul raului, mai degraba decat apa? (Am auzit ca intrebati). Ei bine, in acest caz, intreaga planeta se misca in spate in schimb, iar unele alunecari apar inca (asa cum le-a detectat un spiridon foarte pedantic cu echipamente de masurare implauzibile).

• Inapoi la cuprins

2. Rezistenta

Corpurile care se deplaseaza in fluide incetinesc datorita fortelor rezistive cunoscute sub numele de franare. Aceasta reprezinta de fapt un transfer de impuls din corp catre fluid: lichidul din jur accelereaza in timp ce corpul incetineste, astfel incat momentul total ramane inca constant. Pentru barci, exista diferite tipuri de tragere:

Franare de suprafata,din cauza frecarii dintre corpul de incarcare a apei impreuna cu corpul;
Franare de forma,datorita turbulentelor create de trecerea corpului;
Franare de val ,din cauza pierderii energiei in crearea valurilor.

Modelele de curse sunt neobisnuite in ceea ce priveste faptul ca franarea de suprafata este sursa majora de rezistenta (aproximativ 80%). Pentru cele mai multe alte ambarcatiuni franarea de val domina. De asemenea, aerul contribuie la franarea totala in moduri similare (aerul este doar un alt fluid). In timp ce contributia aerului este doar putin % din rezistenta la apa, viteza aerului este mult mai variabila, astfel incat contributia poate creste pana la 10% din forta vantului puternic.

Franarea de suprafata este proportional cu patratul vitezei, deci daca presupunem ca domina franarea de suprafata, rezistentatotala R poate fi scrisa ca

Unde v2 este patratul vitezei si a este o constanta in functie de suprafata umeda si de forma corpului (adica ramane aceeasi pentru o barca si un echipaj dat).

Pentru a mentine o viteza constanta, forta aplicata trebuie sa fie egala cu rezistenta, astfel incat nu exista nici o acceleratie sau decelerare neta (Legea lui Newton, de fapt, doar pentru a finaliza setul). Prin urmare, puterea medie P necesara (= forta x viteza) este

Acest lucru inseamna ca pentru a dubla viteza barcii, trebuie sa furnizati 23 = 8 ori mai multa putere. Altfel, daca dublezi puterea, te duci doar de 1.26 (= 21/3) ori mai repede. De aceea, vaslitul puternicnu nu te va face sa treci pe langa o echipa care vasleste usor, la fel de repede cum sperati.

• Inapoi la cuprins

3. Energia Cinetica

Folosind exemplul din sectiunea 1, s-ar putea realiza o anumita viteza a ambarcatiunii daca ati mutat o mica cantitate de apa rapid sau o masa mare de apa incet, atata timp cat ritmul total a ramas acelasi. Cu toate acestea, luati in considerare energia cinetica totala U (= ½ x masa x viteza2) ramasa in sistem dupa cursa:

Apoi cele doua exemple dau rezultate diferite.
Daca mw = 10 kg si vw = 10 m / s,

Dar daca mw = 20 kg si vw = 5 m / s,

Aceasta energie cinetica reprezinta lucrul mecanic efectuat de vaslas, dar in primul caz trebuie sa efectueze aproape de doua ori mai multa munca decat cea de-a doua doar pentru a atinge aceeasi viteza.

Pentru a obtine o crestere data a vitezei barcii, este nevoie de mai putina energie pentru a misca o cantitate mare de apa incet decat o cantitate mica de apa rapid. Acesta este argumentul principal in favoarea dimensiunilor lingurilor "mai mari este mai bine" si, de asemenea, pentru a nu se stropii.

• Inapoi la cuprins

4. Centrul de Masa

O barca cu vasle nu este un corp solid - contine trei componente separate:

1. Echipaj, reprezentand 70-80% din masa totala;
2. Corpul, reprezentand 20-30% din masa totala;
3. Intarituri, reprezentand mai putin de 5%, care vor fi ignorate.

Centrul de masa (CM) al intregului sistem este media ponderata a maselor a pozitiilor CM ale fiecarei componente. In timp ce componentele CM individuale se pot deplasa unul fata de celalalt, CM a intregului sistem nu-si poate schimba impulsul (sau viteza) decat daca se aplica forte externe (prin apa, de obicei) (Legea lui Newton din nou).

Daca un echipaj, cu masa mc, sta linistit in spatele unei barci, mb mb deplasandu-se la viteza vt, impulsul total al sistemului este mcvt + mbvt

Daca echipajul incepe apoi sa se deplaseze spre fata la -vc in raport cu vt, barca trebuie sa se deplaseze spre spate la o alta viteza relativa vb pentru a conserva impulsul:

which gives

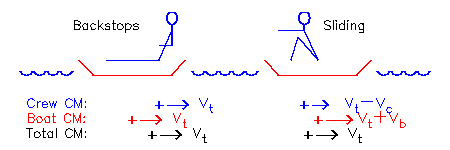Figura (4.1)

Daca echipajul este de 80% din masa totala (adica mc este 4/5 din mc + mb), atunci mc = 4 mb astfel incat vb = 4 vc. In cazul in care echipajul se deplaseaza inapoi cu vc = 0,2 m / s, barca se va deplasa in spate la o valoare suplimentara de 0,8 m / s. In 1 secunda se pare ca echipajul a fost mutat la 1 m spre pupa navei, insa spre un outsider se pare ca 80 cm din acea miscare a fost cu barca care se indrepta spre echipaj.

Acesta este motivul pentru care arcul unei barci pare sa creasca dupa terminarea unei vasliri: desi lamele au fost extrase si nu mai accelereaza sistemul CM al intregului sistem, miscarea echipajului de pe spate accelereaza corpul in fata cu o valoare egala si opusa reactie.

• Inapoi la cuprins

5. Variatia Vitezei

Dependenta de putere a cubului de viteza (Eq.2.2) are o consecinta importanta atunci cand se ia in considerare puterea necesara pentru a mentine o viteza medie.

Daca un echipaj vasleste 1 minut la 4 m / s si apoi 1 minut la 6 m / s, distanta totala pe care o acopera este de 60 x 4 + 60 x 6 = 600 m. Din Eq. (2.2), presupunand ca a = 1 kg / m pentru a mentine sumele simple, lucrul mecanic total W necesar (= putere x timp) este

Iar puterea medie pe cele doua minute (= timp de lucru / timp) este de 140 de wati.Sa presupunem ca acelasi echipaj face doar 2 minute la o constanta de 5 m / s. Acestea vor acoperi aceeasi distanta ca inainte, dar de data aceasta energia totala necesara este diferita

Astfel incat puterea medie este de asemenea redusa, = 125 watti. Deci, au folosit mai putina putere medie (sau mai putina energie totala) pentru a acoperi aceeasi distanta in acelasi timp. Aceasta inseamna ca este mai eficient din punct de vedere energetic sa pastrati acelasi ritm pe parcursul unei curse (sau pe un erg), decat sa porniti repede si sa incetinesti sau sa incepeti incet si sa accelerati.

Figura (5.1)

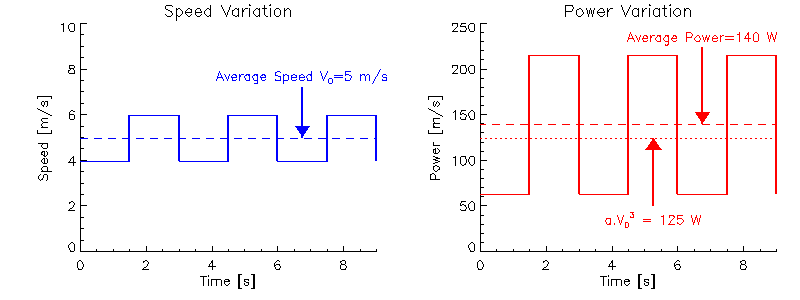Deoarece rezistenta la tractiune a suprafetei (Eq.2.1) depinde mai degraba de viteza cuvei decat de viteza centrului total de masa, aceleasi argumente se aplica si variatiei vitezei cuvei in timpul unei curse (Figura 5.1)).

In cazul in care coca va petrece jumatate din fiecare cursa la 4m / s si jumatate la 6m / s, este mai putin eficient ca mentinerea vitezei constante la 5m / s (obtineti exact acelasi raspuns ca mai sus daca ati impartit piesa de un minut in 60 de parti separate de o secunda intercalate cu 60 x 1 secunde la cealalta viteza). Prin urmare, este de asemenea nedorit sa existe prea multe variatii in viteza cuvei in timpul vaslitului (caracterizata prin ridicarea si coborarea barcii).

In navele "glisante" se fixeaza scaunul cutitului de fixare pe carcasa, insa lanturile si spargatorii sunt conectati si sunt libere sa alunece inapoi si inainte pe rulmenti. Odata cu scullerul care nu mai aluneca in sus si in jos, variatia vitezei corpului prin cursa este redusa, astfel incat aceste barci sunt teoretic mai eficiente (adica merg mai repede pentru aceeasi putere). Din moment ce aceste barci sunt acum interzise, ​​teoria probabil ca a functionat, desi nu neaparat doar datorita argumentelor franare a suprafetei (franarea de val este de asemenea redusa).

• Inapoi la cuprins

6. Echilibru

Barcile plutesc deoarece forta descendenta datorata gravitatiei este exact egalata de forta ascendenta datorata flotabilitatii. Gravitatia actioneaza ca si cum masa totala ar fi concentrata la un singur punct, cunoscut ca centrul de masa sau centrul de greutate (CG). Fortele de flotabilitate actioneaza de asemenea ca si cum ar fi aplicate la un singur punct, cunoscut ca centrul de flotabilitate (CF).

Pe masura ce corpul se roteste, CF se misca in raport cu corpul navei. De exemplu, in figura 6.1, atunci cand corpul este in pozitie verticala, CF se afla de-a lungul liniei intrerupte, dar daca corpul cilindrului este rotit in sens invers acelor de ceasornic (ca in figura), CF se afla de-a lungul liniei punctate. Intersectia liniilor verticale (forte de flotabilitate) prin CF la diferite pozitii de rola se numeste metacentru. Daca forma corpului subacvatic are o sectiune transversala circulara (adica coca cilindrica), metacentrul (M) este pur si simplu in centrul curburii.

Figura (6.1)

Daca un corp pluteste stabil sau instabil pe apa, depinde de pozitiile relative ale metacentrului si ale centrului de greutate.

Figura stanga arata cazul in care M si CG coincid. La orice unghi de rotire, forta de flotabilitate este intotdeauna direct sub forta gravitationala si nu are loc nici un moment de rotatie neta, asadar va sta pe un unghi in care este plasat: "stabil neutru". Un exemplu in acest sens este un cilindru flotant, unde ambele CG si M coincid cu axa centrala.

Figura de mijloc ilustreaza cazul unei cuve de curse. Coca submersa este aproape semi-circulara (pentru a minimiza suprafata: volumul deplasat pentru o anumita latime a liniei de plutire), de unde metacentrul se afla aproape de linia de plutire. Cu toate acestea, pentru a obtine o vaslire eficienta de canotaj, echipajul trebuie sa fie asezat la cativa centimetri deasupra liniei de plutire, astfel incat CG (adica majoritatea echipajului) se afla deasupra lui M. Daca barca se roteste in sens invers acelor de ceasornic, flotabilitatea continua sa actioneze in sus M, dar gravitatia care actioneaza in jos la CG este acum deplasata spre stanga, astfel incat este generat un moment de intoarcere in sensul invers acelor de ceasornic care intareste ruloul - intregul sistem este intrinsec instabil (daca nu credeti asta, luati vasla si vedeti cat timp ramaneti in pozitie verticala).

Figura dreapta arata CG sub M, astfel incat orice rotire in sens invers acelor de ceasornic duce la o miscare CG dreapta fata de M pentru a genera un moment de restaurare in sensul acelor de ceasornic, astfel incat barca este stabila. Un exemplu este o canoe cu canoist asezat jos intr-o barca lata.

Retineti ca stabilitatea este determinata numai de pozitiile relative ale centrului de greutate si ale metacentrelor. Este foarte posibil sa se obtina o stabilitate pentru un vaslas care se afla deasupra liniei de plutire, folosind o coca cu o curbura mai mica (ridicand centrul metacentric spre centrul unui cerc de diametru mai mare - a se vedea figura 6.2). De aceea, barcile de antrenament sunt mai stabile decat barcile de curse. Dezavantajul este cresterea suprafetei pentru aceeasi dislocatie, prin urmare, cresterea franarii.

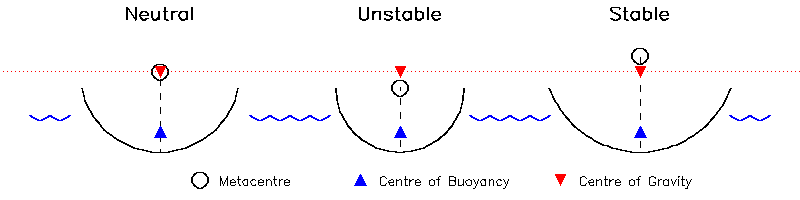Figura (6.2)

Deci, de ce este mai usor sa echilibrezi o barca in miscare? Doua motive:

• Derivorul actioneaza ca un amortizor mai eficient atunci cand apa curge
• Forma arcurilor care se deplaseaza prin apa tinde sa creeze o forta de stabilizare

Vedeti Articolul lui Steve Karr pentru detalii.

• Inapoi la cuprins

7. Parghii

Exista trei clase de parghii in fizica, distinse de cele trei posibile aranjamente liniare ale Osiei, Incarcarea si efortul (lectura de la stanga la dreapta sau de la dreapta la stanga).

1. Incarcare - Fulcrum - Efort
2. Fulcrum - Incarcare - Efort
3. Fulcrum - Efort - Incarcare

Intrucat singura distinctie reala intre osie si sarcina este aceea ca osia este definit ca punct stationar, diferenta dintre parghiile de clasa 1 si 2 depinde de cadrul dvs. de referinta (ce fel de incurcatura a regulamentului FISA ca vaslele trebuie sa fie parghii clasa 2).

Padelele actioneaza ca o parghie care, in cadrul ramei de referinta a ambarcatiunii, apare ca in figura (7.1) ca o parghie de clasa 1:

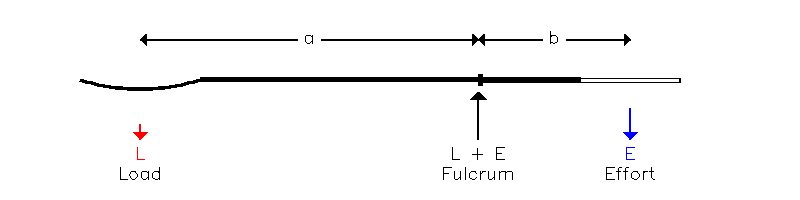Figura (7.1)

Sagetile arata fortele pe padela. Fortele de pe barca (la pin si targa) sunt egale si opuse fortelor de pe vasla de la punctul de sprijin si manerul respectiv, lasand o forta neta L (in jos in figura). Forta propulsiva aplicata pe apa este egala si opusa incarcarii lingurii, de asemenea L (in sus in figura). Prin urmare, fortele de pe barca si apa sunt egale si opuse.

Pentru un anumit efort E, valoarea incarcarii L este determinata de raportul dintre lungimile b si a

Intrucat, pentru o vasla normala, a este mai mare decat b, forta care apare la lama este mai mica decat forta aplicata manerului. Daca aceasta nu pare a fi o idee buna, retineti ca distanta miscata de lama este in mod corespunzator mai mare decat distanta miscata de maner, astfel incat lucrul mecanic W facut la fiecare capat al vaslei, definita ca produsul (forta x Distanta), ramane acelasi. Daca padela este deplasata printr-un unghi y, distanta miscata de maner este b.y si de lama a.y, astfel incat lucrul mecanic efectuat la fiecare capat al vaslei este:

Pentru un observator extern (de exemplu, un oficial FISA aflat pe banca) aceasta situatie pare a fi destul de diferita - partea stationara (= manerul) pare a fi lama mai degraba decat poarta, oferind urmatoarea parghie de clasa 2:

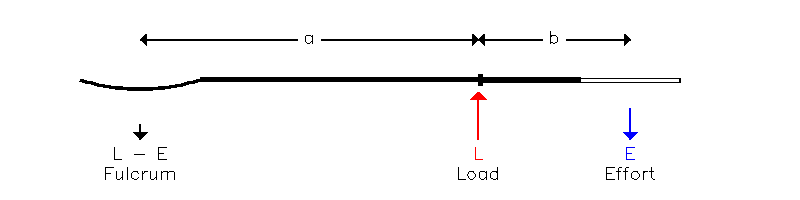Figura (7.2)

In aceasta configuratie sarcina este aplicata la varf si data de raportul dintre lungimea a + b si lungimea a:

In acest caz padela amplifica forta aplicata la maner. Dar retineti ca fortele si directiile de-a lungul vaslei sunt aceleasi ca in Fig. (7.1) ("manerul" si "sarcina" sunt doar etichetate), astfel incat fortele de pe barca si de apa sa ramana aceleasi. Acesta este de fapt un principiu general:

Fortele calculate sunt aceleasi in orice cadru de referinta care se deplaseaza la o viteza constanta.

Cu toate ca este preferabil cadrul de "lama stationara" (figura 7.2), din punctul de vedere al antrenoriatului (de exemplu, invatarea vaslasilor sa manevreze padela peste capatul vasului, in loc sa traga lama prin apa) '(Fig.7.1) are calcule mai usoare, deci o vom folosi atunci cand discutam despre angrenaj in sectiunea urmatoare. Raspunsurile vor fi la fel in orice caz.

• Inapoi la cuprins

8. Angrenaj

Transmisia unei parghii poate fi exprimata pur si simplu ca raportul distantei deplasate de sarcina la distanta miscata de efort, care este, de asemenea, aceeasi cu raportul distantelor dintre sarcina si efort de la maner R (= (A / b)) din Fig. 7.1). Acest raport R determina cat de "usoara" (mica R) sau "grea" (mare R) se simte apa la o viteza specifica a barcii.

Din nefericire, sarcina si efortul pe o vasla nu sunt aplicate in punctele simple definite, astfel incat angrenajul este exprimat conventional in termeni de lungimi care pot fi masurate in mod convenabil.

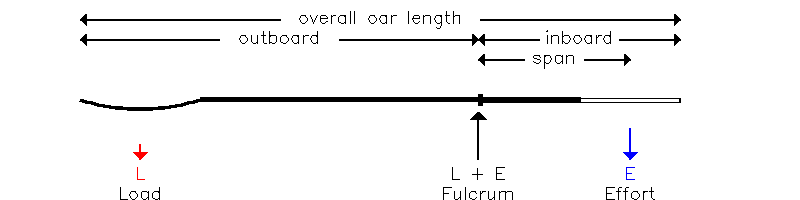Figura (8.1)

Distanta a este de obicei luata ca lungimea exterioara a vaslei (figura 8.1), masurata de la varful lamei pana la partea exterioara a butonului. Cu toate acestea, aceasta este, de obicei, exprimata in termeni de lungime interioara (~ 115 cm), care este mai usor de masurat, si lungimea totala (~ 375 cm), care este (de obicei) fixa (~ 375-115 = 260 cm).

Distanta b este aproximata de intervalul de acoperire, de asemenea cunoscut sub numele de distanta sau TD (distanta de la distanta), care pentru o barca cu bordaj este distanta dintre centrul varfului si linia mediana a barcii (NB Span pentru cranii sunt definite ca fiind duble, adica distanta varf la varf). Retineti ca b nu este definita de lungimea interioara - se presupune ca vaslasul aplica in mod eficient presiunea asupra vaslei de deasupra liniei centrale a barcii, nu la varful manerului.

Pentru a schimba intervalul necesita mutarea varfului in afara (mai usor) sau in interior (mai greu) si are, de asemenea, efectul de a schimba lungimea arcului de vaslire. Detaliile depind de designul riggerilor, dar necesita, de obicei, o sesiune de manipulare majora.

Exista mai multe metode de schimbare a angrenajului prin lungimea exterioara. In ordinea crescatoare a timpului necesar, acestea sunt:

1. Plasati "CLAM" in partea din afara a butoanelor. Acestea sunt in mod eficient butoane suplimentare care scurteaza exteriorul cu aproximativ 1 cm si, prin urmare, usureaza angrenajul.
2. Deplasati butonul in sine spre lingura (mai usor) sau maner (mai greu).
3. Schimbati lungimea vaslei. Pastrarea interiorului vaslei la fel, vasele mai lungi se simt mai grele, iar vasele mai scurte sunt mai usoare.
4. Modificati designul lingurii. Cleaverele aplica in mod eficient incarcatura mai apropiata de varf decat Macons, motiv pentru care cleverii sunt de obicei cu cativa centimetri mai scurti pentru a da o senzatie "echivalenta" pentru acelasi interior si span.

Pentru a gasi schimbarea echivalenta da in exteriorul a care lasa unghiul de transmisie (a / b) neschimbat dupa o schimbare db in interval b:

Deoarece a este de ~ 260cm, b este ~ 85cm, (a / b) este de aproximativ 3, care este factorul de obicei cotat pentru echivalarea modificarilor in intervalul de timp pana la schimbarile in pozitia butonului. De exemplu, cresterea span cu 1 cm ar trebui sa "simta" la fel ca si mutarea butoanelor 3 cm.

• Inapoi la cuprins

Anexa: Legile miscarii lui Newton

• Un corp continua intr-o stare de repaus sau miscare uniforma, daca nu este actionat asupra lui cu o forta externa

• Rata de schimbare a impulsului este proportionala cu Forta aplicata

• Fiecare actiune are o reactie egala si opusa

• Inapoi la cuprins